Новости
Университета Федосеева
Рассылка 4
(продолжение 2)
Тексты расслылок с
картинками выставляются на сайтах:
и т.д.
МНОГОМЕРНАЯ СИСТЕМА
КООРДИНАТ ФЕДОСЕЕВА (МСКФ)
ДЕШГРАММНАЯ ТЕОРИЯ
В основе дешграммной теории лежит мое
изобретение, которое я называю ДЕШГРАММОЙ, а также МНОГОМЕРНАЯ СИСТЕМА
КООРДИНАТ, которую называют МНОГОМЕРНОЙ СИСТЕМОЙ КООРДИНАТ ФЕДОСЕЕВА
(сокращённо – МСКФ), чтобы отличить от всем известной декартовой системы координат.
ДЕШГРАММА - это особым образом
организованная таблица (бланк), которую можно изобразить на плоскости, а также
сделать трёхмерной, то есть изготовить в виде объёмной конструкции.
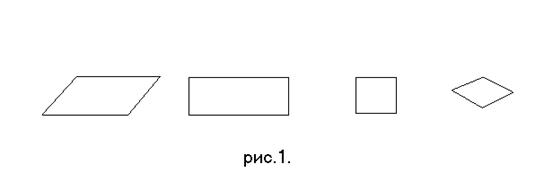
Изобразим на плоскости параллелограмм, в
частности, прямоугольник, или квадрат (см.
рис. 1.). Параллелограмм (прямоугольник, ромб, квадрат) имеет четыре
попарно параллельные стороны. Это четыре отрезка прямых линий, контактирующих
между собой концевыми точками. Между этими отрезками могут быть прямые углы (в
прямоугольнике и квадрате), а могут быть и острые и тупые углы (как в ромбе).
Обозначим числами 0, 1, 2, 3 эти отрезки
прямых линий, образующие параллелограмм, по порядку, начиная, например, с
нижнего по чертежу отрезка и по часовой стрелке (см.
рис. 2.).
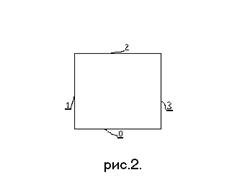
Поле (часть плоскости, например, листа бумаги), на котором изображен параллелограмм, заключенное внутри замкнутой ломаной линии, состоящей из пронумерованных отрезков, назовем ячейкой. Эту одну ячейку будем называть основной.
Договоримся размещать внутри ячейки
какую-либо информацию в виде знаков или рисунков.
Рассмотрим систему переменных (несколько
переменных), каждая из которых может принимать только одно значение. Из
значений этих переменных мы сможем составить всего одну комбинацию. При этом
понятно, что количество комбинаций значений каждой переменной или, попросту,
количество значений каждой переменной, мы приняли за единицу. При этом мы
рассматриваем всю систему в целом, то есть все переменные одновременно. При
этом еще важно подчеркнуть, что каково бы ни было количество таких переменных
(имеющих только одно значение), мы
получим всего одну комбинацию значений всех этих переменных. Понятно, что если
у переменной нет значений, то нет и переменной, следовательно, минимальной
количество значений переменной равно
единице, а максимально количество значений не будем ограничивать, но при
конкретном рассмотрении зафиксируем определенное количество значений.
При этом означенная выше ячейка адекватно
представляет эту одну комбинацию значений переменных (рис. 2.).
Далее, продолжим отрезок под номером
"3" вниз на величину, достаточную для фиксации нашим сознанием факта
увеличения этого отрезка, например, на величину 4 мм.
(см. рис. 3.).
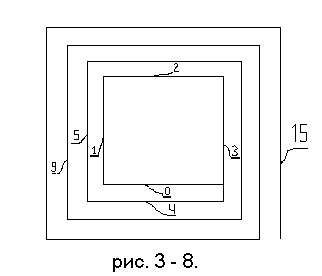
Далее, проведем новую линию, параллельную отрезку под номером "0" и величиной несколько большей, чем этот отрезок (например, на те же 4 мм. (см. рис. 4.). Далее проведем новую линию, параллельную отрезку под
номером "1" и величиной
несколько большей этого отрезка... и т.д. по часовой стрелке. У нас получится
нечто, напоминающее ломаную спираль (см.
рис. 5, рис. 6, рис. 7., рис. 8.).
Продолжим обозначать числами новые отрезки
по порядку по часовой стрелке: 4, 5, 6, 7, 8, 9 и т.д.
Теперь представим себе, что одна из
переменных может принимать два значения. Тогда количество комбинаций значений
всех переменных (подчеркиваем: при любом количестве переменных) будет равно
двум. А изобразить это можно так, как это показано на
рис. 9.
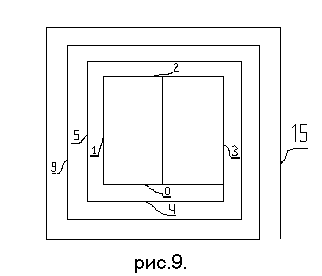
Мы просто делим,
например, "нулевой" отрезок
пополам и проводим линию внутри первоначальной ячейки. Получилось две ячейки,
каждую из которых можно поставить в соответствие с каждой из двух возможных
комбинаций всех значений переменных, сколько бы значений переменных у нас ни
было.
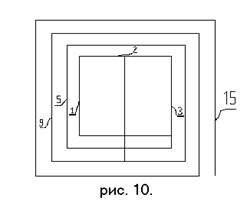
Для примера покажем, что можно присвоить два
значения любой другой переменной, например, переменной под номером
"8" (см. рис.
10.).
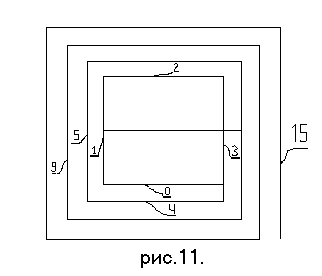
Другой пример см. на рис.
11. Два значения имеет переменная под номером "7".
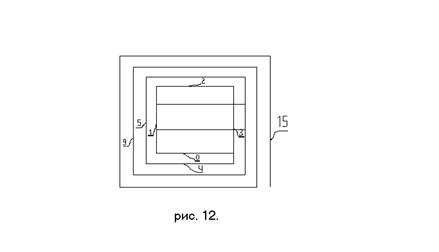
Если какой-нибудь одной переменной присвоить
три, четыре, пять и т. д. значений, то первоначальную ячейку мы разделим на
соответствующее количество частей, проведя соответствующие линии (см. рис. 12., на котором показана
ситуация с тремя значениями одной из переменных). При этом подчеркиваем, что
общее количество комбинаций всех значений всех переменных (сколько бы их не
было) будут равно количеству значений этой переменной.
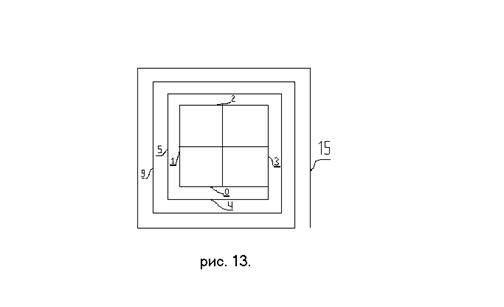
Теперь мы можем представить ситуацию, когда
несколько переменных имеют не одно, а несколько значений.
Например, переменная под номером
"0" имеет два значения и переменная под номером "1" имеет
два значения (см. рис. 13.). Общее количество
комбинаций значений всех переменных будет равно четырем. Количество ячеек равно
количеству этих комбинаций.
Федосеев Роберт Юрьевич